高精度

1. 高精度加法

💡 ( A + B ）( len(A) , len（B） <= $10^6$)

1.1 算法思想：

两个大的数**A + B ( len <= $10^6$)在计算时候，可以使用高精度加法，通过数组的形式存储数位，首先让数组a[ 0 ]**存储各位，数组的最后一位存储最高位以便于相加进位。

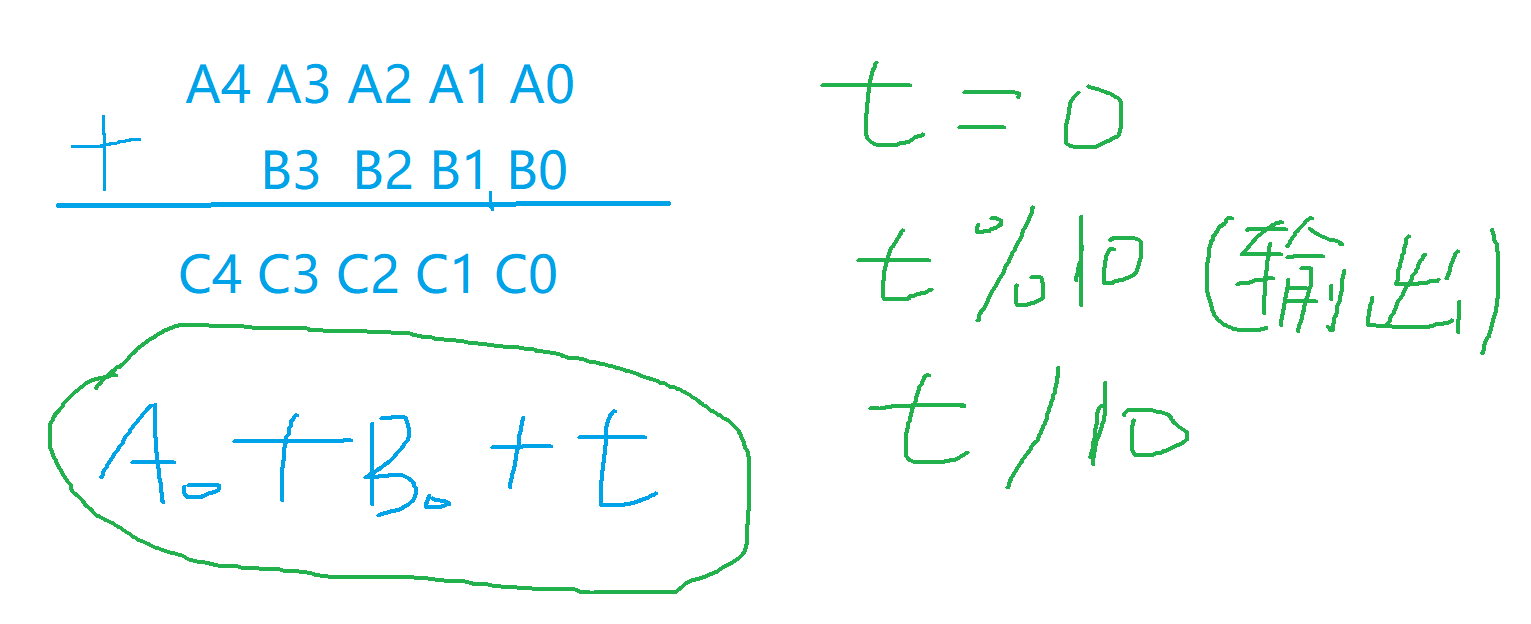
1.2 算法描述：

对于两个高精度的整数 A 和 B 应该是 String类型的。
为了便于相加进位，将数的个位存在 **A[ 0 ]**的位置，数的最高位存在数组的最后一位。
定义进位 int t = 0; 使得 t = A[ i ] + B[ i ] + t ，输出的数为 t % 10 ，然后进位 t 的值为 t / 10
将各个位的数和进位相加，push_back依次存到到数组的最后一位。
按照反位输出。先输出最高位，再输出…..到个位。

1.3 代码模板：

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }

    if (t) C.push_back(t);
    return C;
}

2. 高精度减法

💡 ( A - B ）( len(A) , len（B） <= $10^6$)

2.1 算法思想：

两个大的数**A - B ( len <= $10^6$)在计算时候，可以使用高精度减法，通过数组的形式存储数位，（同高精度加法一样，反位存储数列）首先让数组a[ 0 ]**存储各位，数组的最后一位存储最高位以便于相加进位。

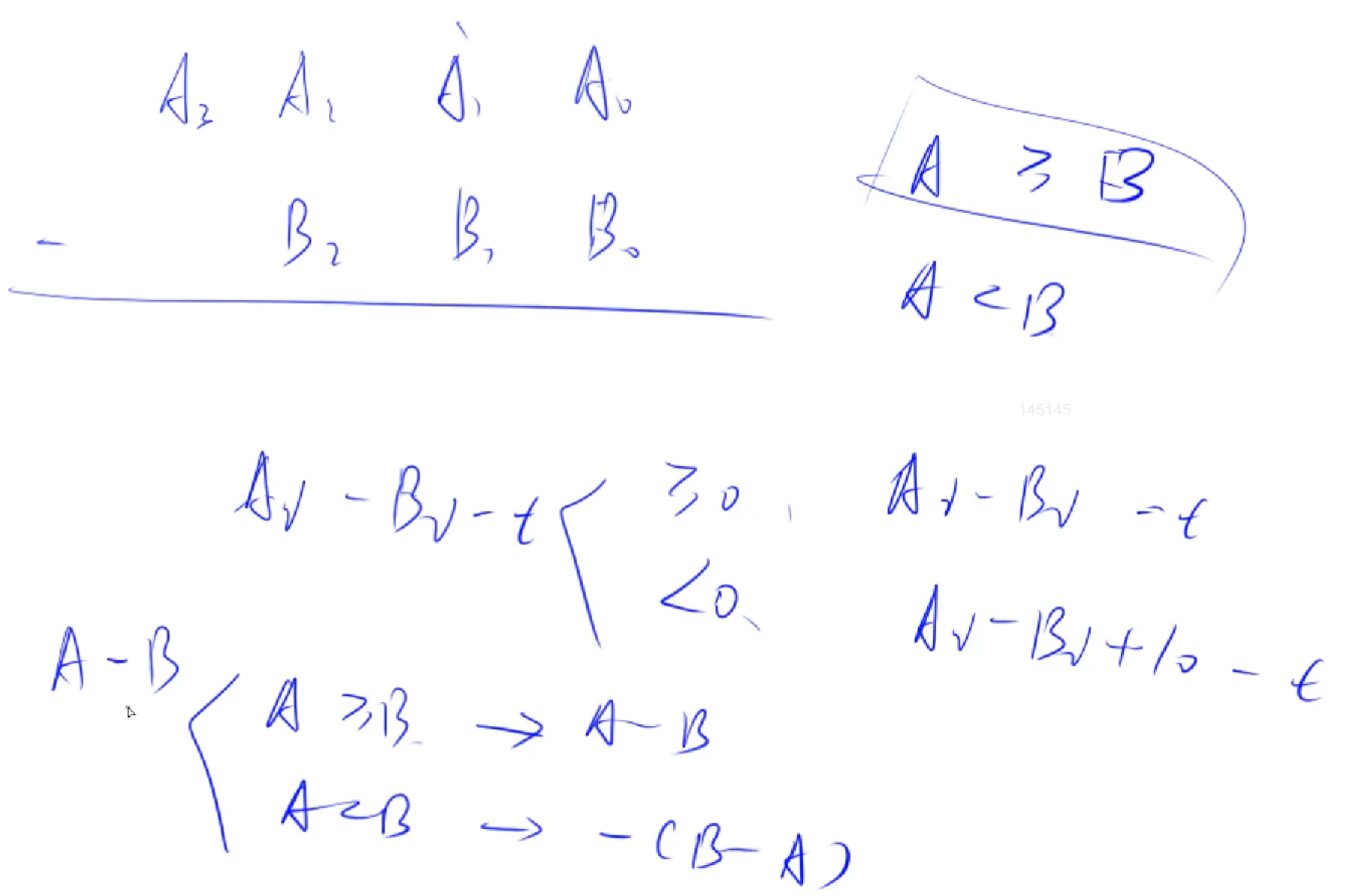
2.2 算法描述：

对于两个高精度的整数 A 和 B 应该是 String类型的。
为了便于相减借位后结果的长度变短，将数的个位存在 **A[ 0 ]**的位置，数的最高位存在数组的最后一位。
定义进位 int t = 0; 使得 t = A[ i ] - B[ i ] - t （ t >= 0）或t = A[ i ] - B[ i ] + 10 - t （ t <0），**输出的数为**( ( t + 10 ) % 10)，**因为当 **t >= 0 时，得到的数仍为 t ，当 t < 0 时，得到的值为 t 借位后相减的值
将各个位的数和进位相减，push_back依次存到数组的最后一位。
按照反位输出。先输出最高位，再输出…..到个位。

2.3 代码模板：

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

3. 高精度乘低精度

💡 ( A * b ）( len(A) <= $10^6$ , b <= 10000 )

3.1算法的思想：

一个大整数 A 和一个小整数 b 相乘，A 的每一位数 A [ i ]*乘以 **b** 得到的数加上进位 **t** ，然后*%10**就是该位的结果（既（ C [ i ] = A [ i ] * b）%10）**, **t [ i ] = ( A [ i ] * b ) / 10**，得到的每一位**C [ i ]**就是相乘得到的结果。

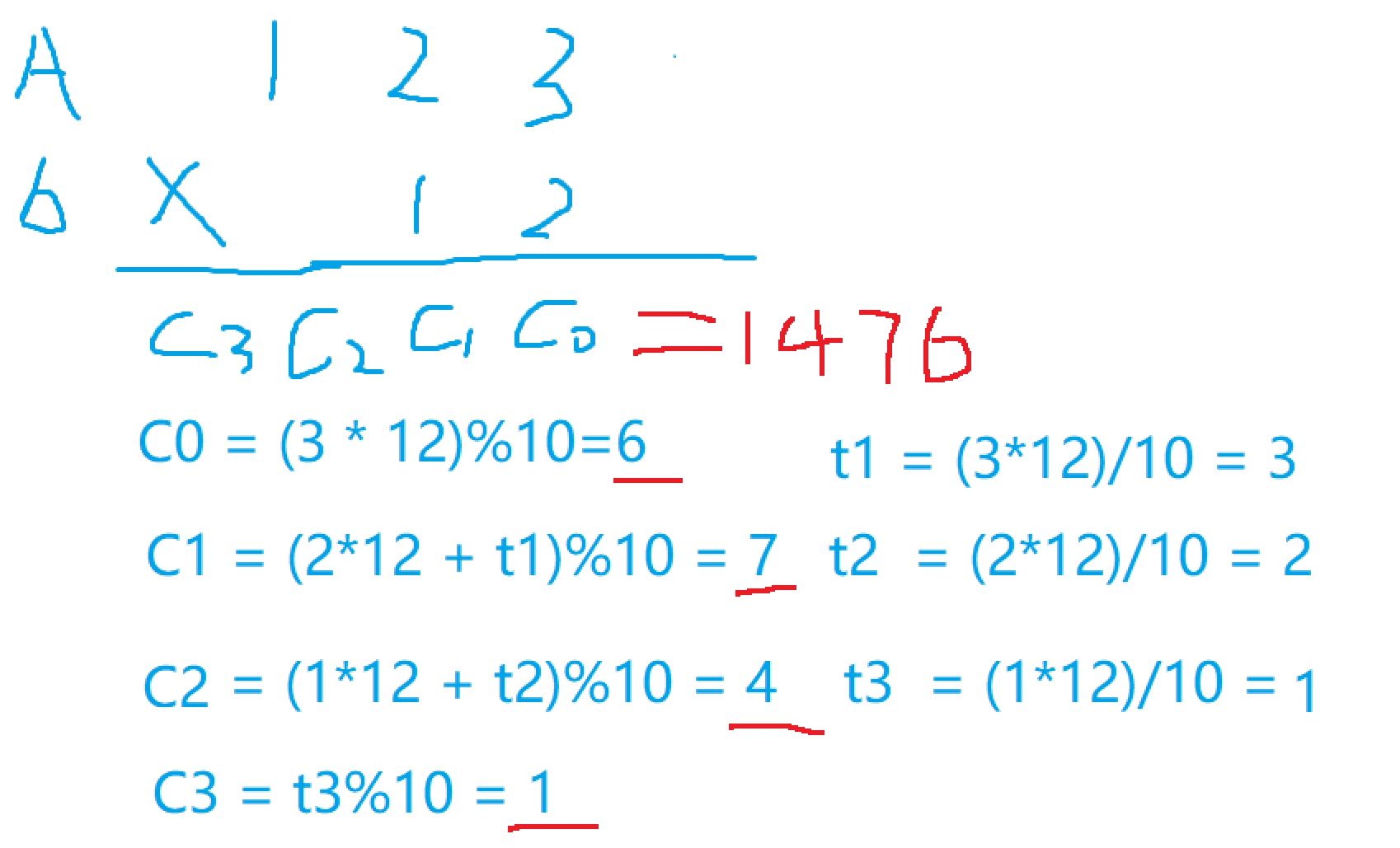
3.2 算法描述：

一个大整数 A 是String类型乘以一个小整数 b （b <=10000 ）
倒叙存入数组每一位数
结果的每一位数 C [ i ] = A [ i ] * b）%10
每一个数的进位 t [ i ] = ( A [ i ] * b ) / 10
倒叙输出

3.3 代码模板：

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

4. 高精度除法

💡 ( A / b ）( len(A) <= $10^6$ , b <= 10000 )

4.1 算法的思想：

一个大整数 A 除以一个小整数 b ,得到商和余数，余数为 r = r * 10 + A[i] ;每一位的商为C.push_back =（ r / b）, 然后再使 r = r % b 这里可以正序存储法，但是考虑到一个运算中包含了加减乘除，所以使用倒叙存储也是可以的，最后只需要使用reverse（）函数反转一下就OK。

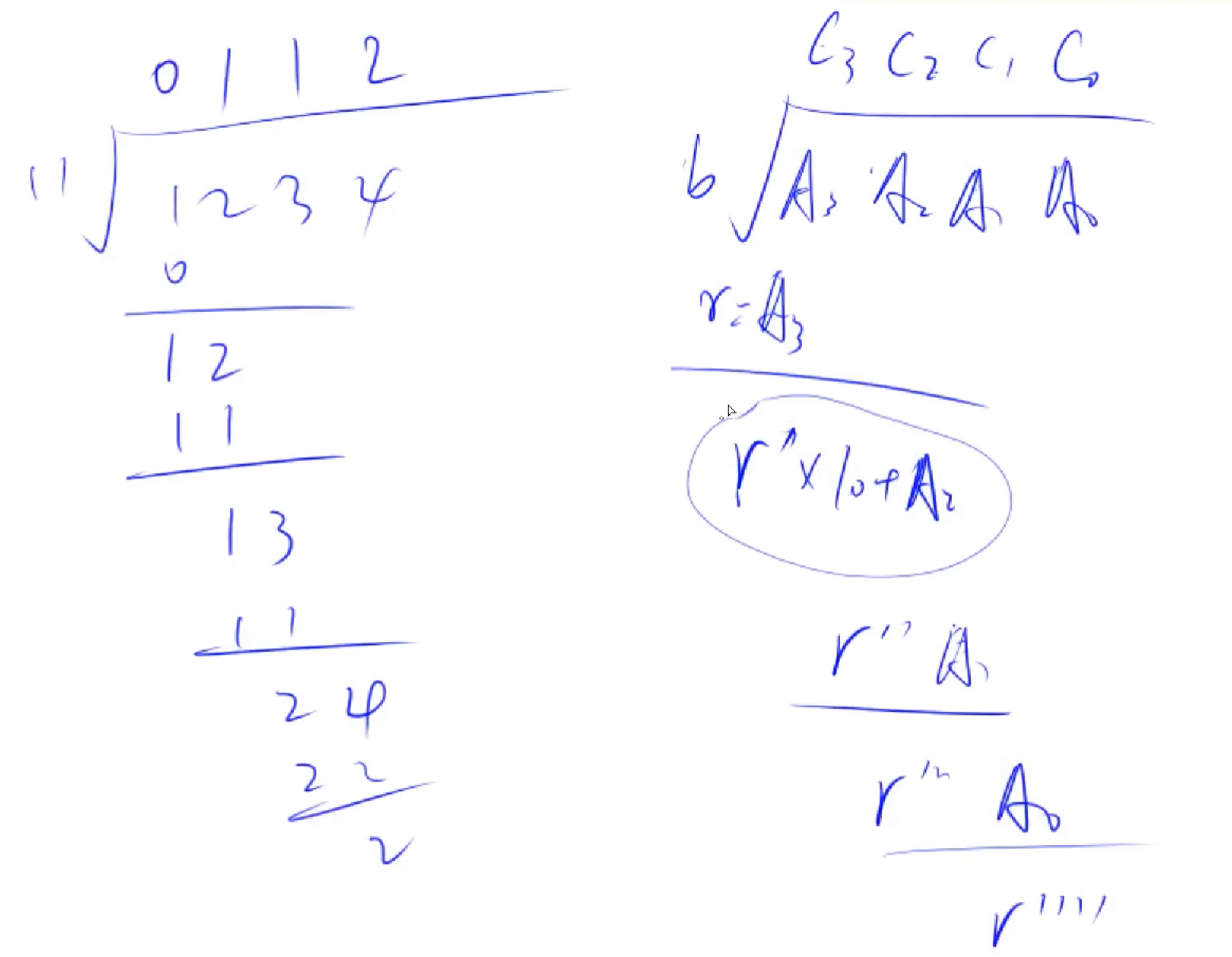
4.2 算法描述：

一个大整数 A 是String类型乘以一个小整数 b （b <=10000 ）
倒叙存入数组每一位数（也可以正序存，为了考虑混合运算中包含加减乘除，所以使用倒叙）
先算余数，再算商。
每一个数的余数 r = r * 10 + A[i]
结果的每一位数 C [ i ] = r / b
倒叙输出

4.3 代码模板：

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

苦逼小码农

https://spicypig.top/2023/05/23/High-precision/