拓扑排序

💡 拓扑排序思想：有向无环图（DAG图）

1. 拓扑排序算法思想：

拓扑排序是指将一个有向无环图(Directed Acyclic Graph简称DAG)进行排序进而得到一个有序的线性序列。利用拓扑排序可以将事件按照顺序排序后进行处理，可以确定事件发生的先后顺序。我们把入度为 0 的那些顶点放入 queue 中，然后通过每次执行 queue 中的顶点，就可以让依赖这个被执行的顶点的那些点的 入度-1，如果有顶点的入度变成了 0，就可以放入 queue 了，直到 queue 为空。

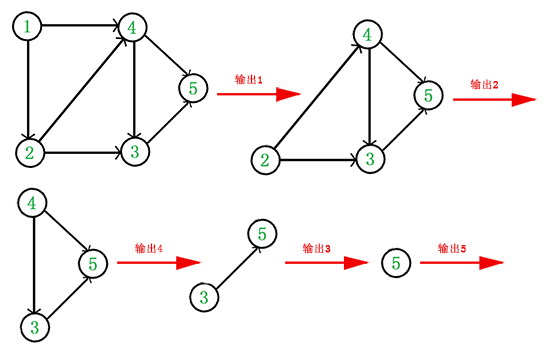
拓扑排序必须为有向无环图

拓扑排序中存在度

• 例如3的入度（既指向3的边的个数）\是*2，出度（从3指出的边的个数）*是**1

2. 拓扑排序算法实现方式：

• 把入度为0的点放入一个queue中， 然后就需要把某些点拿出去执行了，把 C1 拿出来执行，那这意味「以 C1 为顶点」的「指向其他点」的「边」都消失了，也就是 C1 的出度变成了 0.

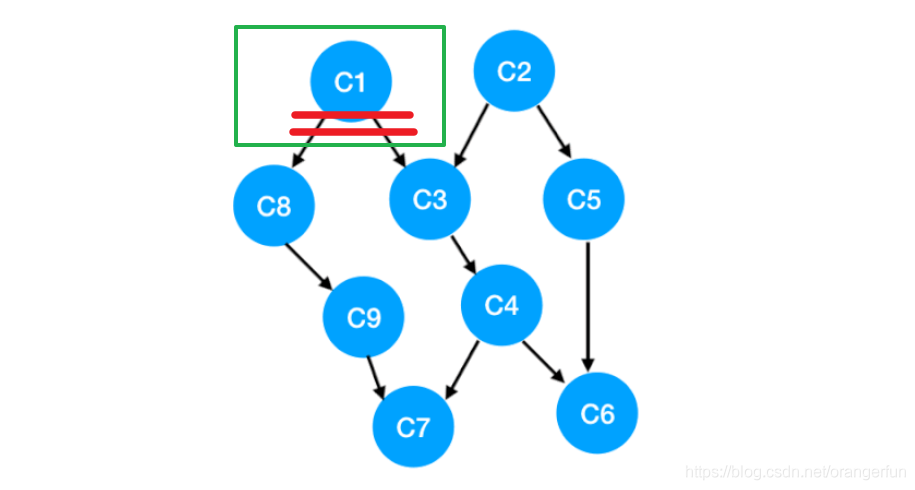
此时我们更新了C3和C8点的入度：（此时队列中的数为C2，C8）

	c3	c4	c5	c6	c7	c8	c9
入度	1	2	1	2	2	0	1

• 下一个我们再执行 C2，C2 所指向的 C3, C5 的 入度就要减一

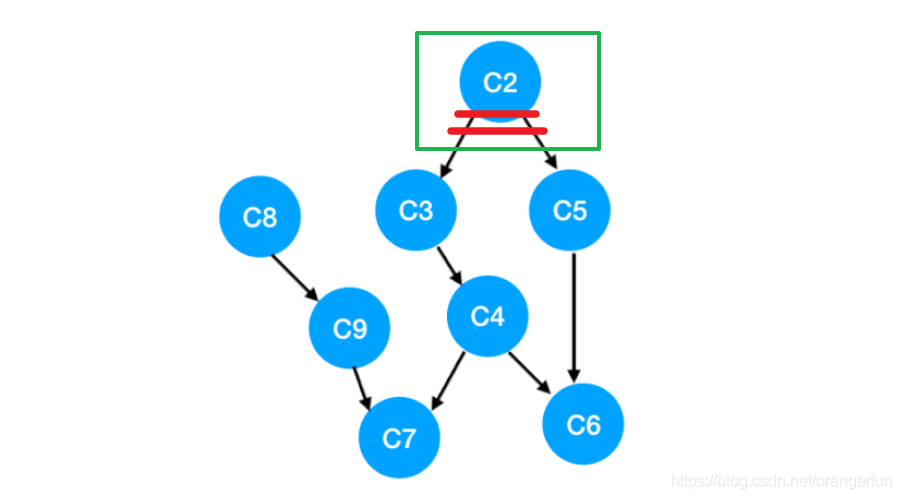
更新表格：（此时队列中的数为C8，C3, C5）

	c3	c4	c5	c6	c7	c9
入度	0	2	0	2	2	1

• 如此继续执行，直到queue为空即可

3. 拓扑排序代码模板：

拓扑排序 —— 模板题 AcWing 848. 有向图的拓扑序列
时间复杂度 O(n+m)O(n+m), nn 表示点数，mm 表示边数
bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}