二分查找
1.整数二分
💡 时间复杂度:$logN$
(a)快速排序算法实现方式:
有单调性一定可以二分,可以二分不一定有单调性
二分查找是通过将一个有序序列划分为两个区间,通过不断的缩小区间的大小在不同的区间寻找答案的一种方式,相比与顺序查找效率高了很多,缺点是二分之前要对数据进行排序,耗时。
二分查找要求:线性表是有序表,即表中结点按关键字有序,并且要用向量作为表的存储结构 。二分我们需要确定一个区间,使得目标在一定的区间中。
二分满足的性质:
- 具有二段性(一段满足,另一段不满足)
- 答案是二分的分界点
整数二分分为两种情况:
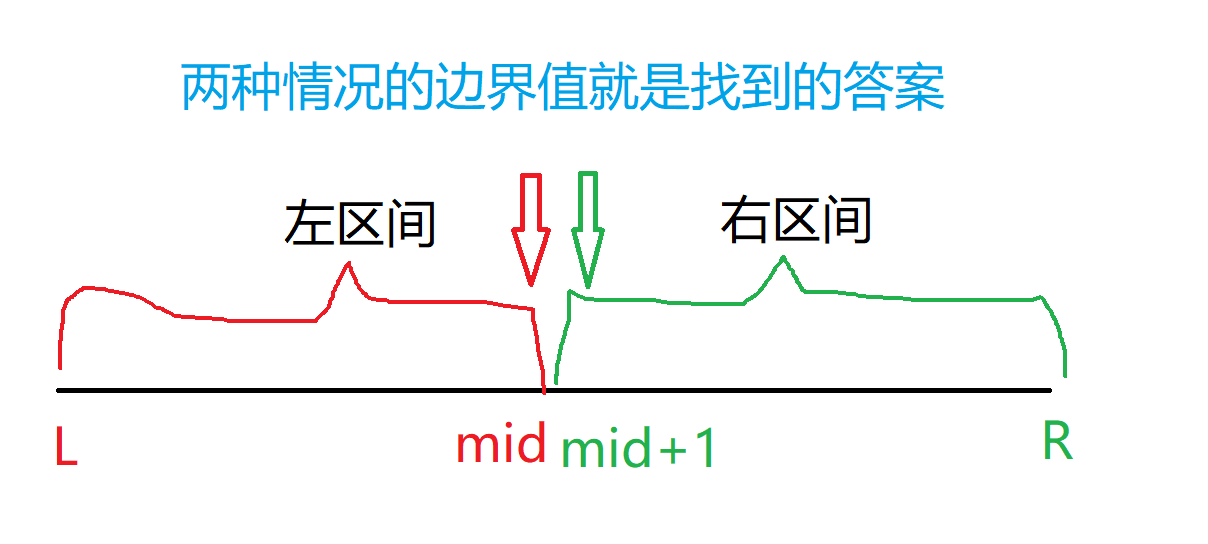

(b)算法描述:
首先确定该区间的中点位置
将待查的X值与q[mid]比较:若相等,则查找成功并返回此位置,否则须确定新的查找区间,继续二分查找
① 若q[mid] > X,将查找区间变为[ L , mid - 1 ]
②若q[mid] < X,将查找区间变为[ mid + 1 , R ]
假设目标值在 [ L ,R ]中,每次查找区间将缩小一半,当 L = R 时,我们就找到了目标。
(c)整数二分查找代码模板:
版本一:
当我们将区间[l, r]划分为[l, mid]和[mid + 1, r]时,其更新操作是r = mid 或 l = mid + 1,计算mid时不需要加1。
bool check( int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}版本二:
当我们将区间[l, r]划分为[l, mid - 1]和[mid, r]时,其更新操作是l = mid - 1或 l = mid,计算mid时需要加1。
bool check( int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}2. 浮点数二分
(a)浮点数二分查找代码模板:
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}


